树，作为五大经典数据结构之一，有许多运用场景，比如MySQL数据库的B+树（数据结构的重要性不用强调了吧）。下面将对二叉树、红黑树、B树、B+树等树结构进行一些概念区分与总结，此篇博客适合新手、有一定数据结构基础的小伙伴。
根据子节点的个数可以划分成N叉树（一般N ≥ 2），N叉树拥有的特征是每个节点至多有N个子节点。
比如，N = 2时，称为二叉树，每个节点至多只有2个节点。
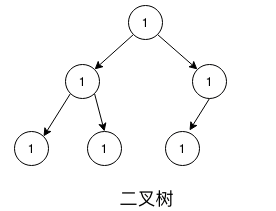比如，N = 3时，称为三叉树，每个节点至多只有3个节点。
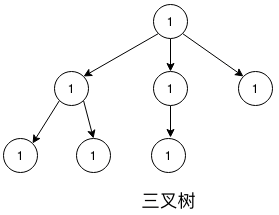$\color{red}注意：$特别的当N = 1时，此时是"一叉树"（一般没有这个概念，这只是我个人这么叫），其实"一叉树"就是链表。
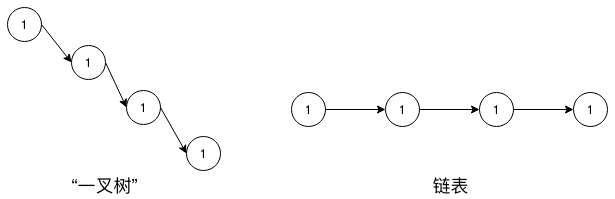还有一点，树的定义并不是很严谨，因为它强调的是每个节点至多有N个子节点，那么，如果某N叉树的每个节点都至多只有N - 1个节点，那么它也可以称为N - 1叉树，反过来，它也可以称为K叉树（K ≥ N）。
由上面的概念可知，当N = 2时，称为二叉树。在二叉树还有左子树、右子树、左孩子、右孩子的概念。
由二叉树的结构可知，每个节点都是由左子节点、右子节点、父节点构成（有些节点的左或右子节点为空，但不能说它没有左或右子节点）。根据节点的访问顺序可排列出 左父右、左右父、父左右、右父左、右左父、父右左6种情况，但是一般要求左子节点比右子节点先访问，因此剩下 左父右、左右父、父左右三种情况。
左父右） 对于每个节点，先访问它的左子树，再访问本节点，最后访问它的右子树，对于左子树、右子树也符合这个规定（递归定义）。
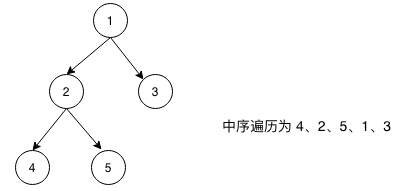关于二叉树的中序遍历算法实现，请参考我先前的博客 LeetCode 二叉树的中序遍历（递归和非递归算法）
左右父） 对于每个节点，先访问它的左子树，再访问它的右子树，最后访问本节点，对于左子树、右子树也符合这个规定（递归定义）。
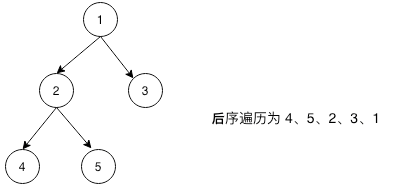关于二叉树的后序遍历算法实现，请参考我先前的博客 LeetCode 二叉树的后序遍历（递归、递推）
父左右） 对于每个节点，先访问本节点，再访问它的左子树，最后访问它的右子树，对于左子树、右子树也符合这个规定（递归定义）。
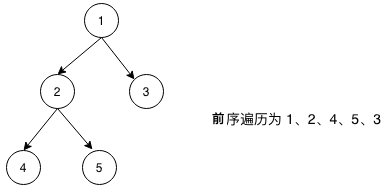关于二叉树的先序遍历算法实现，请参考我先前的博客 LeetCode 二叉树的前序遍历（递归、递推）
$\color{red}注：$其实还有一种遍历方式，层次遍历，即按层访问二叉树。请参考我先前的博客 LeetCode 二叉树的层次遍历
二叉搜索树的定义是对于某二叉树的每个节点b，它的左子树A的所有节点的值都小于节点b的值，它的右子树B的所有节点的值都大于节点b的值，并且左子树A、右子树B同样符合这个定义（递归定义）。
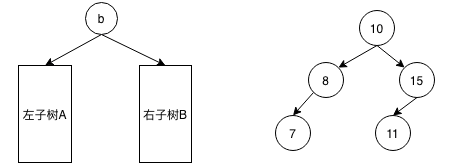对于值为10的节点，左子树的所有节点的值 < 10，右子树的所有节点的值 > 10，并且左子树、右子树中的所有节点同样 左 < 父 < 右 的定义。
$\color{red}表现特征：$二叉搜索树的定义简化一下就是左 < 父 < 右规则，还记先前介绍的中序遍历么，是不是发现了什么，中序遍历顺序不也是如此么。其实二叉搜索树的变现特征就是中序遍历得到的序列递增。（==可能会有小伙伴问，为什么要引入这个特性呢？答案是查找方便。如果我们需要你在二叉树中查target = 7这个值是否存在，从根节点入手，如果target = root，查找成功，停止查找；若target < root，转到左子树，否则target > root，转到右子树。==）
平衡二叉树定义是某二叉树的左、右两个子树的 ==高度差的绝对值不超过1==，并且左、右两个子树也都是一棵平衡二叉树（递归定义）。
那么问题来了，为啥又要引入平衡这个概念呢？
可以看出平衡主要是限制树的整体高度，将左、右子树的高度差缩减到1之内。
平衡二叉搜索树，顾名思义，是二叉树同时满足平衡二叉树以及二叉搜索树的定义，即二叉树不但中序遍历为递增序列，并且树还平衡。
问题又来了，引入平衡二叉搜索树又是为啥目的捏？看完下图你就明白了。
上图左边的树是平衡二叉搜索树，右边是一颗非平衡的二叉搜索树。如果给你这两颗树，让你搜索target = 15，你会选择那一颗？你肯定会选择左边的吧，因为它看起来更矮一些，根据上面介绍的二叉搜索树的查找规则，我们每次都大概能排除掉剩余节点中的一半（最优的情况下，搜索复杂度为==log~2~n==）。
得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，其实它就是上面介绍的平衡二叉搜索树。
由于平衡二叉搜索树的定义比较苛刻，实际过程中生成并维持一颗平衡二叉搜索树是比较复杂的，而红黑树放宽了平衡条件的限制，引入弱平衡的概念。
红黑树的定义： 1.节点是红色或黑色。 2.根是黑色。 3.所有叶子都是黑色（叶子是NIL节点）。 4.每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。） 5.从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点（简称黑高）。
关于红黑树的更多维护细节，请参考我的博客 数据结构之红黑树（还在为看不懂红黑树而烦恼吗？别再翻了，此篇足矣~）
根据先前树的划分，对于多叉树也有父节点、子节点、兄弟节点的概念。
Trie树其实就是前缀树，运用于大量字符串的存放。
关于Trie树的运用，请参考我先前的博客 LeetCode 前缀和后缀搜索（前缀树）
其实Trie树的关键就是把每个字符串的前缀进行合并，也称前缀树。
$\color{red}注意：$在Trie树中，每个节点的子节点可能有26个，因为对于每个字符串的下一个字符可能是a ~ z中的任意字母。并且26个子节点需要保持有序。
B树是多路搜索树，对于树中的非叶子节点，如果放了m个关键字，就同时需要放m+1个指向子节点的指针，根节点的子节点数为[2, N]，其他节点的子节点数为[N/2,N]。并且所有关键字在整颗树中只出现一次，非叶子结点可以命中所有叶子结点位于同一层。
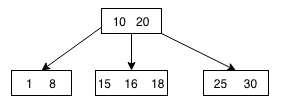
B+树是在B树上进行改造升级，把叶子节点层串成一个链表，并且父节点修改为每个子节点关键字序列的最大值。
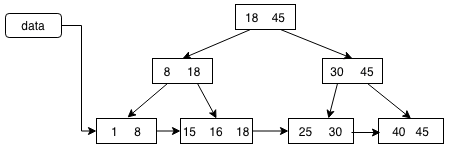
MySQL数据库的表结构底层数据存储用的就是B+树。
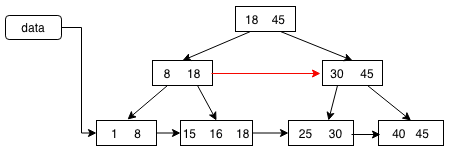
B*树是在B+树的基础上再次进行升级，把非叶子节点层也用串成链表。
个人总结：AVL树、红黑树都是二叉树，并且是平衡二叉搜索树，Trie树、B树、B+树、B*树都是多叉树，并且是多叉搜索树。一般编程算法题中，二叉树使用的较多。对于多叉树，除非是专业的数据结构设计人员，用的是比较少的，但是这并不说明多叉树没有用武之地，文章中多次提及MySQL数据库中的表中的数据就是用B+树存储。（本博客多叉树用的篇幅很少，但是B树、B+树等多叉树的插入、删除节点是比较复杂的，可能会涉及到节点的拆分、合并，但是博主能力有限啊）
以上就是数据结构之二叉树、红黑树、B树、B+树、Trie树浅析的主要内容。
已更新二叉搜索树、红黑树维护博客，欢迎阅读。 数据结构之二叉搜索树详解（附C++代码实现查找、插入、删除操作） 数据结构之红黑树（还在为看不懂红黑树而烦恼吗？别再翻了，此篇足矣~）